З давніх-давен людина використовувала пристрої, що допомагають виконувати роботу, яка потребує зусиль, що значно перевищують природні можливості м’язів людини. Використовуючи знання про перерозподіл сил, люди створили прості механізми, які дозволяють виконувати більшу роботу з меншими витратами енергії.
Пристрої, призначені для збільшення сили або зміни її напрямку, називаються механізмами. До механізму прикладається сила, яку він передає тілам, переміщуючи їх та виконуючи роботу.
До простих механізмів належать важіль, блок, похила площина, коловорот, клин, гвинт, колесо та інші.
Похилу площину використовували ще під час будівництва єгипетських пірамід. Вона застосовується і зараз для підйому на незначну висоту.
Важкі речі можна підняти за допомогою довгого дерев’яного або металевого стрижня, що має точку опори. Він називається важелем. За принципом важеля працює, наприклад, криниця «журавель». З важелів складається скелет людини і тварин. Спосіб прикріплення м’язів до кісток забезпечує кінцівкам тварин швидкість руху, що має велике значення для життя тварин у природі.
Важкі валізи, сумки легше нести удвох, тримаючи їх на якомусь стрижні тому що таким чином рівномірно розподіляються сили тяжіння. Розподіл сил буде не однаковим, якщо вантаж переносять люди різного зросту. У такому випадку нахил стрижня змінить поділ сил і людина меншого зросту буде відчувати дію сили більше. Таким чином, змінивши точку дії сили‚ можна змінити кількісні показники сили.
За допомогою блоків можна підняти вантаж угору на значну висоту, використовуючи лише силу м’язів. Блок — це коліщатко з жолобом посередині. Воно кріпиться на вісь і тому може обертатись. Через жолобок перекинута мотузка. Людина, використовуючи вагу свого тіла, може тягти мотузку вниз, а вантаж буде підніматися вгору, що значно легше, ніж нести його в руках. Блок не дає виграшу в силі, але дозволяє змінити напрямок дії сили.
Коловорот теж простий механізм. Його і зараз використовують для підйому води з колодязів, у лебідках.
Клин — це трикутний механізм, виготовлений із дерева або металу. За допомогою клину легше розколоти дерев’яні колоди, каміння.
Механізми, які складаються з двох або більше простих механізмів, з’єднаних між собою, називаються складними. Прикладом складного механізму можуть бути звичайні ножиці. Вони складаються з двох з’єднаних між собою важелів, заточених у вигляді клина. Також до складних механізмів належить домкрат, що складається з важеля та гвинта.
Механізмом у фізиці називається прилад для перетворення сили (її збільшення або зменшення). Наприклад, докладаючи невелике зусилля в одному місці механізму, можна отримати значно більше зусилля в іншому його місці. Один вид механізму нам вже зустрівся: це гідравлічний прес. Тут ми розглянемо так звані прості механізми – важіль і похилу площину.
Важіль
Важіль – це тверде тіло, яке може обертатися навколо нерухомої осі. На рис. 1 зображений важіль з віссю обертання O. До кінців важеля (точкам A і B) прикладені сили і
. Плечі цих сил рівні відповідно
і
.
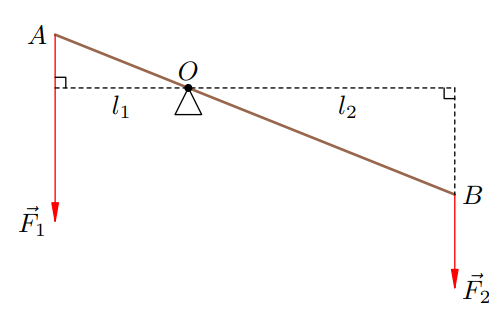
Умова рівноваги важеля дається правилом моментів : , звідки
З цього співвідношення виходить, що важіль дає виграш в силі або у відстані (дивлячись, з якою метою він використовується) в стільки разів, в скільки більше плече довше за менше.
Наприклад, щоб зусиллям 100 Н підняти вантаж вагою 700 Н, треба узяти важіль з відношенням плечей 7 : 1 і покласти вантаж на коротке плече. Ми виграємо в силі в 7 разів, але в стільки ж разів програємо у відстані: кінець довгого плеча опише в 7 разів більшу дугу, ніж кінець короткого плеча (тобто вантаж).
Прикладами важеля, що дає виграш в силі, являються лопата, ножиці, плоскогубці. Весло весляра – це важіль, що дає виграш у відстані. А звичайні важільні ваги є рівноплечим важелем, що не дає виграшу ні у відстані, ні в силі (інакше їх можна використати для обважування покупців).
Нерухомий блок
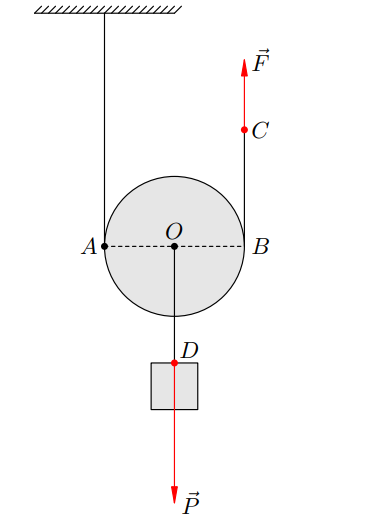
Важливим різновидом важеля є блок – закріплене в обоймі колесо з жолобом, по якому пропущений мотузок. У більшості завач мотузок вважається невагомою нерозтяжною ниткою. На рис. 2 зображений нерухомий блок, тобто блок з нерухомою віссю обертання (що проходить перпендикулярно до площини рисунка через точку O).

На правому кінці нитки в точці D закріплений вантаж вагою
До лівого кінця нитки в точці C прикладена сила . Плече сили
рівне OA =
, де
– радіус блоку. Плече ваги
рівне OB =
. Значить, нерухомий блок є рівноплечим важелем і тому не дає виграшу ні в силі, ні у відстані: по-перше, маємо рівність
, а по-друге, в процесі руху вантажу і нитки переміщення точки C дорівнює переміщенню вантажу.
Навіщо ж тоді взагалі потрібний нерухомий блок? Він корисний тим, що дозволяє змінити напрям зусилля. Зазвичай нерухомий блок використовується як частину складніших механізмів.
На рис. 3 зображений рухомий блок, вісь якого переміщається разом з вантажем. Ми тягнемо за нитку з силою , яка прикладена в точці C і спрямована вгору. Блок обертається і при цьому також рухається вгору, піднімаючи вантаж, підвішений на нитці OD. В даний момент часу нерухомою точкою є точка A, і саме навколо неї обертається блок (він як би “перекочується” через точку A).
Говорять, що через точку A проходить миттєва вісь обертання блоку (ця вісь спрямована перпендикулярно до площини малюнка). Вага вантажу прикладена в точці D кріплення вантажу до нитки. Плече сили
рівне AO =
. А плече сили
, з якою ми тягнемо за нитку, є в два разі більшим : воно рівне AB =
. Відповідно, умовою рівноваги вантажу є рівність
(що ми і бачимо на рис. 3: довжина вектору
у два рази менша за довжину вектора
).
Отже, рухомий блок дає виграш в силі в два рази. При цьому ми в ті ж два рази програємо у відстані. Дійсно, неважко зрозуміти, що для підняття вантажу на один метр точку C доведеться перемістити вгору на два метри (тобто витягнути два метри нитки).
Блоку на рис. 3 має один недолік: тягнути нитку вгору (за точку C) – не найкраща ідея. Погодьтеся, що набагато зручніше тягнути за нитку вниз! Ось тут-то нас і виручає нерухомий блок. На мал. 4 зображений підйомний механізм, який є комбінацією рухомого блоку з нерухомим. До рухомого блоку підвішений вантаж, а трос додатково перекинутий через нерухомий блок, що дає можливість тягнути за трос вниз для підйому вантажу вгору.
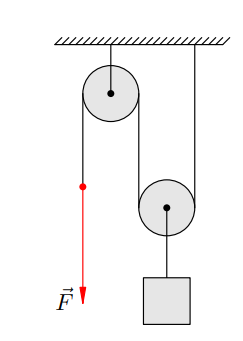
Зовнішнє зусилля на тросі знову позначене вектором . Принципово цей пристрій нічим не відрізняється від рухомого блоку: з його допомогою ми також отримуємо двократний виграш в силі.
Площина похилої
Як ми знаємо, важку бочку простіше викотити по похилих містках, ніж піднімати вертикально. Містки, таким чином, є механізмом, який дає виграш в силі. У механіці подібний механізм називається похилою площиною. Похила площина – це рівна плоска поверхня, розташована під деяким кутом до горизонту. У такому разі коротко говорять: “похила площина з кутом
“.
Знайдемо силу, яку потрібно прикласти до вантажу маси , щоб рівномірно підняти його по гладкій похилій площині з кутом
. Ця сила
, зрозуміло, спрямована уздовж похилої площини (рис. 5).
Виберемо вісь X так, як показано на малюнку. Оскільки вантаж рухається без прискорення, сили, що діють на нього, урівноважені:
Проектуємо на вісь X:
звідки
Саме таку силу треба прикласти, щоб рухати вантаж вгору по похилій площині. Щоб рівномірно піднімати той же вантаж по вертикалі, до нього треба прикласти силу, рівну . Видно, що
<
, оскільки
< 1. Похила площина дійсно дає виграш в силі, і тим більший, чим менший кут
. Широко вживаними різновидами похилої площини є клин і гвинт.
Золоте правило механіки
Простий механізм може дати виграш в силі або у відстані, але не може дати виграшу в роботі. Наприклад, важіль з відношенням плечей 2 : 1 дає виграш в силі в два рази. Щоб на меншому плечі підняти вантаж вагою ![]() , треба до більшого плеча прикласти силу
, треба до більшого плеча прикласти силу . Але для підняття вантажу на висоту
більше плече доведеться опустити на
, і виконана робота буде рівна
,
тобто тій же величині, що і без використання важеля.
У разі похилої площини ми виграємо в силі, оскільки прикладаємо до вантажу силу , меншу сили тяжіння. Проте, щоб підняти вантаж на висоту
над початковим положенням, нам треба пройти шлях
уздовж похилої площини. При цьому ми здійснюємо роботу
тобто ту ж саму, що і при вертикальному піднятті вантажу.
Ці факти служать проявами так званого золотого правила механіки.
Золоте правило механіки. Жоден з простих механізмів не дає виграшу в роботі. У скільки разів виграємо в силі, в стільки ж разів програємо у відстані, і навпаки. Золоте правило механіки є не що інше, як простий варіант закону збереження енергії.
Домашнє завдання: опрацювати параграф 36, задачу 4 ст.236.

Немає коментарів:
Дописати коментар